Fiscal Risk and Government Debt¶
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
Overview¶
This lecture studies government debt in an AMSS economy [AMSSeppala02] of the type described in Optimal Taxation without State-Contingent Debt.
We study the behavior of government debt as time $ t \rightarrow + \infty $.
We use these techniques
- simulations
- a regression coefficient from the tail of a long simulation that allows us to verify that the asymptotic mean of government debt solves a fiscal-risk minimization problem
- an approximation to the mean of an ergodic distribution of government debt
- an approximation to the rate of convergence to an ergodic distribution of government debt
We apply tools that are applicable to more general incomplete markets economies that are presented on pages 648 - 650 in section III.D of [BEGS17] (BEGS).
We study an AMSS economy [AMSSeppala02] with three Markov states driving government expenditures.
- In a previous lecture, we showed that with only two Markov states, it is possible that endogenous interest rate fluctuations eventually can support complete markets allocations and Ramsey outcomes.
- The presence of three states prevents the full spanning that eventually prevails in the two-state example featured in Fiscal Insurance via Fluctuating Interest Rates.
The lack of full spanning means that the ergodic distribution of the par value of government debt is nontrivial, in contrast to the situation in Fiscal Insurance via Fluctuating Interest Rates in which the ergodic distribution of the par value of government debt is concentrated on one point.
Nevertheless, [BEGS17] (BEGS) establish that, for general settings that include ours, the Ramsey planner steers government assets to a level that comes as close as possible to providing full spanning in a precise a sense defined by BEGS that we describe below.
We use code constructed in Fluctuating Interest Rates Deliver Fiscal Insurance.
Warning: Key equations in [BEGS17] section III.D carry typos that we correct below.
Let’s start with some imports:
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.optimize import minimize
The Economy¶
As in Optimal Taxation without State-Contingent Debt and Optimal Taxation with State-Contingent Debt, we assume that the representative agent has utility function
$$ u(c,n) = {\frac{c^{1-\sigma}}{1-\sigma}} - {\frac{n^{1+\gamma}}{1+\gamma}} $$We work directly with labor supply instead of leisure.
We assume that
$$ c_t + g_t = n_t $$The Markov state $ s_t $ takes three values, namely, $ 0,1,2 $.
The initial Markov state is $ 0 $.
The Markov transition matrix is $ (1/3) I $ where $ I $ is a $ 3 \times 3 $ identity matrix, so the $ s_t $ process is IID.
Government expenditures $ g(s) $ equal $ .1 $ in Markov state $ 0 $, $ .2 $ in Markov state $ 1 $, and $ .3 $ in Markov state $ 2 $.
We set preference parameters
$$ \begin{aligned} \beta & = .9 \cr \sigma & = 2 \cr \gamma & = 2 \end{aligned} $$The following Python code sets up the economy
import numpy as np
class CRRAutility:
def __init__(self,
β=0.9,
σ=2,
γ=2,
π=0.5*np.ones((2, 2)),
G=np.array([0.1, 0.2]),
Θ=np.ones(2),
transfers=False):
self.β, self.σ, self.γ = β, σ, γ
self.π, self.G, self.Θ, self.transfers = π, G, Θ, transfers
# Utility function
def U(self, c, n):
σ = self.σ
if σ == 1.:
U = np.log(c)
else:
U = (c**(1 - σ) - 1) / (1 - σ)
return U - n**(1 + self.γ) / (1 + self.γ)
# Derivatives of utility function
def Uc(self, c, n):
return c**(-self.σ)
def Ucc(self, c, n):
return -self.σ * c**(-self.σ - 1)
def Un(self, c, n):
return -n**self.γ
def Unn(self, c, n):
return -self.γ * n**(self.γ - 1)
First and Second Moments¶
We’ll want first and second moments of some key random variables below.
The following code computes these moments; the code is recycled from Fluctuating Interest Rates Deliver Fiscal Insurance.
def mean(x, s):
'''Returns mean for x given initial state'''
x = np.array(x)
return x @ u.π[s]
def variance(x, s):
x = np.array(x)
return x**2 @ u.π[s] - mean(x, s)**2
def covariance(x, y, s):
x, y = np.array(x), np.array(y)
return x * y @ u.π[s] - mean(x, s) * mean(y, s)
Long Simulation¶
To generate a long simulation we use the following code.
We begin by showing the code that we used in earlier lectures on the AMSS model.
Here it is
import numpy as np
from scipy.optimize import root
from quantecon import MarkovChain
class SequentialAllocation:
'''
Class that takes CESutility or BGPutility object as input returns
planner's allocation as a function of the multiplier on the
implementability constraint μ.
'''
def __init__(self, model):
# Initialize from model object attributes
self.β, self.π, self.G = model.β, model.π, model.G
self.mc, self.Θ = MarkovChain(self.π), model.Θ
self.S = len(model.π) # Number of states
self.model = model
# Find the first best allocation
self.find_first_best()
def find_first_best(self):
'''
Find the first best allocation
'''
model = self.model
S, Θ, G = self.S, self.Θ, self.G
Uc, Un = model.Uc, model.Un
def res(z):
c = z[:S]
n = z[S:]
return np.hstack([Θ * Uc(c, n) + Un(c, n), Θ * n - c - G])
res = root(res, 0.5 * np.ones(2 * S))
if not res.success:
raise Exception('Could not find first best')
self.cFB = res.x[:S]
self.nFB = res.x[S:]
# Multiplier on the resource constraint
self.ΞFB = Uc(self.cFB, self.nFB)
self.zFB = np.hstack([self.cFB, self.nFB, self.ΞFB])
def time1_allocation(self, μ):
'''
Computes optimal allocation for time t >= 1 for a given μ
'''
model = self.model
S, Θ, G = self.S, self.Θ, self.G
Uc, Ucc, Un, Unn = model.Uc, model.Ucc, model.Un, model.Unn
def FOC(z):
c = z[:S]
n = z[S:2 * S]
Ξ = z[2 * S:]
# FOC of c
return np.hstack([Uc(c, n) - μ * (Ucc(c, n) * c + Uc(c, n)) - Ξ,
Un(c, n) - μ * (Unn(c, n) * n + Un(c, n)) \
+ Θ * Ξ, # FOC of n
Θ * n - c - G])
# Find the root of the first-order condition
res = root(FOC, self.zFB)
if not res.success:
raise Exception('Could not find LS allocation.')
z = res.x
c, n, Ξ = z[:S], z[S:2 * S], z[2 * S:]
# Compute x
I = Uc(c, n) * c + Un(c, n) * n
x = np.linalg.solve(np.eye(S) - self.β * self.π, I)
return c, n, x, Ξ
def time0_allocation(self, B_, s_0):
'''
Finds the optimal allocation given initial government debt B_ and
state s_0
'''
model, π, Θ, G, β = self.model, self.π, self.Θ, self.G, self.β
Uc, Ucc, Un, Unn = model.Uc, model.Ucc, model.Un, model.Unn
# First order conditions of planner's problem
def FOC(z):
μ, c, n, Ξ = z
xprime = self.time1_allocation(μ)[2]
return np.hstack([Uc(c, n) * (c - B_) + Un(c, n) * n + β * π[s_0]
@ xprime,
Uc(c, n) - μ * (Ucc(c, n)
* (c - B_) + Uc(c, n)) - Ξ,
Un(c, n) - μ * (Unn(c, n) * n
+ Un(c, n)) + Θ[s_0] * Ξ,
(Θ * n - c - G)[s_0]])
# Find root
res = root(FOC, np.array(
[0, self.cFB[s_0], self.nFB[s_0], self.ΞFB[s_0]]))
if not res.success:
raise Exception('Could not find time 0 LS allocation.')
return res.x
def time1_value(self, μ):
'''
Find the value associated with multiplier μ
'''
c, n, x, Ξ = self.time1_allocation(μ)
U = self.model.U(c, n)
V = np.linalg.solve(np.eye(self.S) - self.β * self.π, U)
return c, n, x, V
def Τ(self, c, n):
'''
Computes Τ given c, n
'''
model = self.model
Uc, Un = model.Uc(c, n), model.Un(c, n)
return 1 + Un / (self.Θ * Uc)
def simulate(self, B_, s_0, T, sHist=None):
'''
Simulates planners policies for T periods
'''
model, π, β = self.model, self.π, self.β
Uc = model.Uc
if sHist is None:
sHist = self.mc.simulate(T, s_0)
cHist, nHist, Bhist, ΤHist, μHist = np.zeros((5, T))
RHist = np.zeros(T - 1)
# Time 0
μ, cHist[0], nHist[0], _ = self.time0_allocation(B_, s_0)
ΤHist[0] = self.Τ(cHist[0], nHist[0])[s_0]
Bhist[0] = B_
μHist[0] = μ
# Time 1 onward
for t in range(1, T):
c, n, x, Ξ = self.time1_allocation(μ)
Τ = self.Τ(c, n)
u_c = Uc(c, n)
s = sHist[t]
Eu_c = π[sHist[t - 1]] @ u_c
cHist[t], nHist[t], Bhist[t], ΤHist[t] = c[s], n[s], x[s] / u_c[s], \
Τ[s]
RHist[t - 1] = Uc(cHist[t - 1], nHist[t - 1]) / (β * Eu_c)
μHist[t] = μ
return np.array([cHist, nHist, Bhist, ΤHist, sHist, μHist, RHist])
import numpy as np
from scipy.optimize import fmin_slsqp
from scipy.optimize import root
from quantecon import MarkovChain
class RecursiveAllocationAMSS:
def __init__(self, model, μgrid, tol_diff=1e-7, tol=1e-7):
self.β, self.π, self.G = model.β, model.π, model.G
self.mc, self.S = MarkovChain(self.π), len(model.π) # Number of states
self.Θ, self.model, self.μgrid = model.Θ, model, μgrid
self.tol_diff, self.tol = tol_diff, tol
# Find the first best allocation
self.solve_time1_bellman()
self.T.time_0 = True # Bellman equation now solves time 0 problem
def solve_time1_bellman(self):
'''
Solve the time 1 Bellman equation for calibration model and
initial grid μgrid0
'''
model, μgrid0 = self.model, self.μgrid
π = model.π
S = len(model.π)
# First get initial fit from Lucas Stokey solution.
# Need to change things to be ex ante
pp = SequentialAllocation(model)
interp = interpolator_factory(2, None)
def incomplete_allocation(μ_, s_):
c, n, x, V = pp.time1_value(μ_)
return c, n, π[s_] @ x, π[s_] @ V
cf, nf, xgrid, Vf, xprimef = [], [], [], [], []
for s_ in range(S):
c, n, x, V = zip(*map(lambda μ: incomplete_allocation(μ, s_), μgrid0))
c, n = np.vstack(c).T, np.vstack(n).T
x, V = np.hstack(x), np.hstack(V)
xprimes = np.vstack([x] * S)
cf.append(interp(x, c))
nf.append(interp(x, n))
Vf.append(interp(x, V))
xgrid.append(x)
xprimef.append(interp(x, xprimes))
cf, nf, xprimef = fun_vstack(cf), fun_vstack(nf), fun_vstack(xprimef)
Vf = fun_hstack(Vf)
policies = [cf, nf, xprimef]
# Create xgrid
x = np.vstack(xgrid).T
xbar = [x.min(0).max(), x.max(0).min()]
xgrid = np.linspace(xbar[0], xbar[1], len(μgrid0))
self.xgrid = xgrid
# Now iterate on Bellman equation
T = BellmanEquation(model, xgrid, policies, tol=self.tol)
diff = 1
while diff > self.tol_diff:
PF = T(Vf)
Vfnew, policies = self.fit_policy_function(PF)
diff = np.abs((Vf(xgrid) - Vfnew(xgrid)) / Vf(xgrid)).max()
print(diff)
Vf = Vfnew
# Store value function policies and Bellman Equations
self.Vf = Vf
self.policies = policies
self.T = T
def fit_policy_function(self, PF):
'''
Fits the policy functions
'''
S, xgrid = len(self.π), self.xgrid
interp = interpolator_factory(3, 0)
cf, nf, xprimef, Tf, Vf = [], [], [], [], []
for s_ in range(S):
PFvec = np.vstack([PF(x, s_) for x in self.xgrid]).T
Vf.append(interp(xgrid, PFvec[0, :]))
cf.append(interp(xgrid, PFvec[1:1 + S]))
nf.append(interp(xgrid, PFvec[1 + S:1 + 2 * S]))
xprimef.append(interp(xgrid, PFvec[1 + 2 * S:1 + 3 * S]))
Tf.append(interp(xgrid, PFvec[1 + 3 * S:]))
policies = fun_vstack(cf), fun_vstack(
nf), fun_vstack(xprimef), fun_vstack(Tf)
Vf = fun_hstack(Vf)
return Vf, policies
def Τ(self, c, n):
'''
Computes Τ given c and n
'''
model = self.model
Uc, Un = model.Uc(c, n), model.Un(c, n)
return 1 + Un / (self.Θ * Uc)
def time0_allocation(self, B_, s0):
'''
Finds the optimal allocation given initial government debt B_ and
state s_0
'''
PF = self.T(self.Vf)
z0 = PF(B_, s0)
c0, n0, xprime0, T0 = z0[1:]
return c0, n0, xprime0, T0
def simulate(self, B_, s_0, T, sHist=None):
'''
Simulates planners policies for T periods
'''
model, π = self.model, self.π
Uc = model.Uc
cf, nf, xprimef, Tf = self.policies
if sHist is None:
sHist = simulate_markov(π, s_0, T)
cHist, nHist, Bhist, xHist, ΤHist, THist, μHist = np.zeros((7, T))
# Time 0
cHist[0], nHist[0], xHist[0], THist[0] = self.time0_allocation(B_, s_0)
ΤHist[0] = self.Τ(cHist[0], nHist[0])[s_0]
Bhist[0] = B_
μHist[0] = self.Vf[s_0](xHist[0])
# Time 1 onward
for t in range(1, T):
s_, x, s = sHist[t - 1], xHist[t - 1], sHist[t]
c, n, xprime, T = cf[s_, :](x), nf[s_, :](
x), xprimef[s_, :](x), Tf[s_, :](x)
Τ = self.Τ(c, n)[s]
u_c = Uc(c, n)
Eu_c = π[s_, :] @ u_c
μHist[t] = self.Vf[s](xprime[s])
cHist[t], nHist[t], Bhist[t], ΤHist[t] = c[s], n[s], x / Eu_c, Τ
xHist[t], THist[t] = xprime[s], T[s]
return np.array([cHist, nHist, Bhist, ΤHist, THist, μHist, sHist, xHist])
class BellmanEquation:
'''
Bellman equation for the continuation of the Lucas-Stokey Problem
'''
def __init__(self, model, xgrid, policies0, tol, maxiter=1000):
self.β, self.π, self.G = model.β, model.π, model.G
self.S = len(model.π) # Number of states
self.Θ, self.model, self.tol = model.Θ, model, tol
self.maxiter = maxiter
self.xbar = [min(xgrid), max(xgrid)]
self.time_0 = False
self.z0 = {}
cf, nf, xprimef = policies0
for s_ in range(self.S):
for x in xgrid:
self.z0[x, s_] = np.hstack([cf[s_, :](x),
nf[s_, :](x),
xprimef[s_, :](x),
np.zeros(self.S)])
self.find_first_best()
def find_first_best(self):
'''
Find the first best allocation
'''
model = self.model
S, Θ, Uc, Un, G = self.S, self.Θ, model.Uc, model.Un, self.G
def res(z):
c = z[:S]
n = z[S:]
return np.hstack([Θ * Uc(c, n) + Un(c, n), Θ * n - c - G])
res = root(res, 0.5 * np.ones(2 * S))
if not res.success:
raise Exception('Could not find first best')
self.cFB = res.x[:S]
self.nFB = res.x[S:]
IFB = Uc(self.cFB, self.nFB) * self.cFB + \
Un(self.cFB, self.nFB) * self.nFB
self.xFB = np.linalg.solve(np.eye(S) - self.β * self.π, IFB)
self.zFB = {}
for s in range(S):
self.zFB[s] = np.hstack(
[self.cFB[s], self.nFB[s], self.π[s] @ self.xFB, 0.])
def __call__(self, Vf):
'''
Given continuation value function next period return value function this
period return T(V) and optimal policies
'''
if not self.time_0:
def PF(x, s): return self.get_policies_time1(x, s, Vf)
else:
def PF(B_, s0): return self.get_policies_time0(B_, s0, Vf)
return PF
def get_policies_time1(self, x, s_, Vf):
'''
Finds the optimal policies
'''
model, β, Θ, G, S, π = self.model, self.β, self.Θ, self.G, self.S, self.π
U, Uc, Un = model.U, model.Uc, model.Un
def objf(z):
c, n, xprime = z[:S], z[S:2 * S], z[2 * S:3 * S]
Vprime = np.empty(S)
for s in range(S):
Vprime[s] = Vf[s](xprime[s])
return -π[s_] @ (U(c, n) + β * Vprime)
def objf_prime(x):
epsilon = 1e-7
x0 = np.asfarray(x)
f0 = np.atleast_1d(objf(x0))
jac = np.zeros([len(x0), len(f0)])
dx = np.zeros(len(x0))
for i in range(len(x0)):
dx[i] = epsilon
jac[i] = (objf(x0+dx) - f0)/epsilon
dx[i] = 0.0
return jac.transpose()
def cons(z):
c, n, xprime, T = z[:S], z[S:2 * S], z[2 * S:3 * S], z[3 * S:]
u_c = Uc(c, n)
Eu_c = π[s_] @ u_c
return np.hstack([
x * u_c / Eu_c - u_c * (c - T) - Un(c, n) * n - β * xprime,
Θ * n - c - G])
if model.transfers:
bounds = [(0., 100)] * S + [(0., 100)] * S + \
[self.xbar] * S + [(0., 100.)] * S
else:
bounds = [(0., 100)] * S + [(0., 100)] * S + \
[self.xbar] * S + [(0., 0.)] * S
out, fx, _, imode, smode = fmin_slsqp(objf, self.z0[x, s_],
f_eqcons=cons, bounds=bounds,
fprime=objf_prime, full_output=True,
iprint=0, acc=self.tol, iter=self.maxiter)
if imode > 0:
raise Exception(smode)
self.z0[x, s_] = out
return np.hstack([-fx, out])
def get_policies_time0(self, B_, s0, Vf):
'''
Finds the optimal policies
'''
model, β, Θ, G = self.model, self.β, self.Θ, self.G
U, Uc, Un = model.U, model.Uc, model.Un
def objf(z):
c, n, xprime = z[:-1]
return -(U(c, n) + β * Vf[s0](xprime))
def cons(z):
c, n, xprime, T = z
return np.hstack([
-Uc(c, n) * (c - B_ - T) - Un(c, n) * n - β * xprime,
(Θ * n - c - G)[s0]])
if model.transfers:
bounds = [(0., 100), (0., 100), self.xbar, (0., 100.)]
else:
bounds = [(0., 100), (0., 100), self.xbar, (0., 0.)]
out, fx, _, imode, smode = fmin_slsqp(objf, self.zFB[s0], f_eqcons=cons,
bounds=bounds, full_output=True,
iprint=0)
if imode > 0:
raise Exception(smode)
return np.hstack([-fx, out])
import numpy as np
from scipy.interpolate import UnivariateSpline
class interpolate_wrapper:
def __init__(self, F):
self.F = F
def __getitem__(self, index):
return interpolate_wrapper(np.asarray(self.F[index]))
def reshape(self, *args):
self.F = self.F.reshape(*args)
return self
def transpose(self):
self.F = self.F.transpose()
def __len__(self):
return len(self.F)
def __call__(self, xvec):
x = np.atleast_1d(xvec)
shape = self.F.shape
if len(x) == 1:
fhat = np.hstack([f(x) for f in self.F.flatten()])
return fhat.reshape(shape)
else:
fhat = np.vstack([f(x) for f in self.F.flatten()])
return fhat.reshape(np.hstack((shape, len(x))))
class interpolator_factory:
def __init__(self, k, s):
self.k, self.s = k, s
def __call__(self, xgrid, Fs):
shape, m = Fs.shape[:-1], Fs.shape[-1]
Fs = Fs.reshape((-1, m))
F = []
xgrid = np.sort(xgrid) # Sort xgrid
for Fhat in Fs:
F.append(UnivariateSpline(xgrid, Fhat, k=self.k, s=self.s))
return interpolate_wrapper(np.array(F).reshape(shape))
def fun_vstack(fun_list):
Fs = [IW.F for IW in fun_list]
return interpolate_wrapper(np.vstack(Fs))
def fun_hstack(fun_list):
Fs = [IW.F for IW in fun_list]
return interpolate_wrapper(np.hstack(Fs))
def simulate_markov(π, s_0, T):
sHist = np.empty(T, dtype=int)
sHist[0] = s_0
S = len(π)
for t in range(1, T):
sHist[t] = np.random.choice(np.arange(S), p=π[sHist[t - 1]])
return sHist
Next, we show the code that we use to generate a very long simulation starting from initial government debt equal to $ -.5 $.
Here is a graph of a long simulation of 102000 periods.
μ_grid = np.linspace(-0.09, 0.1, 100)
log_example = CRRAutility(π=(1 / 3) * np.ones((3, 3)),
G=np.array([0.1, 0.2, .3]),
Θ=np.ones(3))
log_example.transfers = True # Government can use transfers
log_sequential = SequentialAllocation(log_example) # Solve sequential problem
log_bellman = RecursiveAllocationAMSS(log_example, μ_grid,
tol=1e-12, tol_diff=1e-10)
T = 102000 # Set T to 102000 periods
sim_seq_long = log_sequential.simulate(0.5, 0, T)
sHist_long = sim_seq_long[-3]
sim_bel_long = log_bellman.simulate(0.5, 0, T, sHist_long)
titles = ['Government Debt', 'Tax Rate']
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
for ax, title, id in zip(axes.flatten(), titles, [2, 3]):
ax.plot(sim_seq_long[id], '-k', sim_bel_long[id], '-.b', alpha=0.5)
ax.set(title=title)
ax.grid()
axes[0].legend(('Complete Markets', 'Incomplete Markets'))
plt.tight_layout()
plt.show()
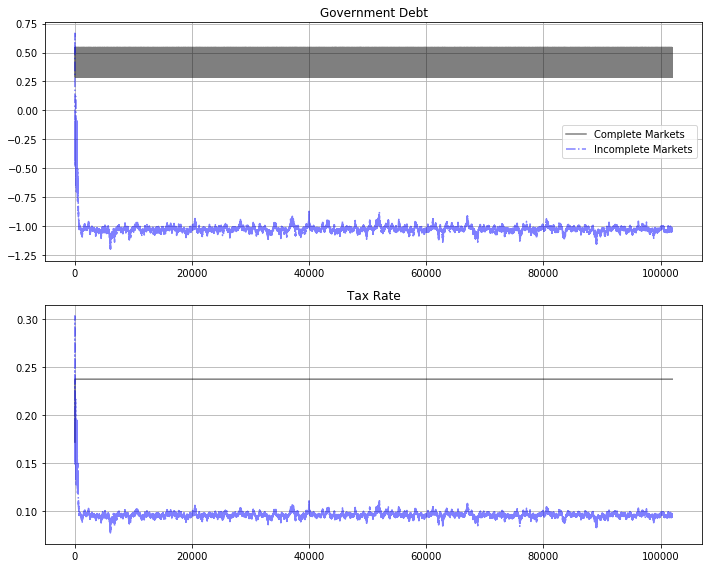
The long simulation apparently indicates eventual convergence to an ergodic distribution.
It takes about 1000 periods to reach the ergodic distribution – an outcome that is forecast by approximations to rates of convergence that appear in BEGS [BEGS17] and that we discuss in Fluctuating Interest Rates Deliver Fiscal Insurance.
Let’s discard the first 2000 observations of the simulation and construct the histogram of the par value of government debt.
We obtain the following graph for the histogram of the last 100,000 observations on the par value of government debt.
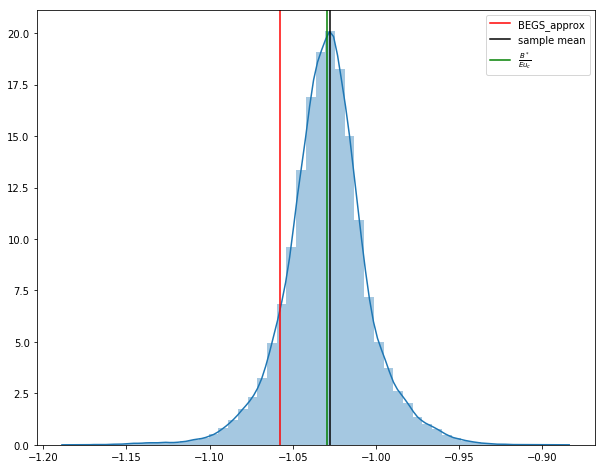
The black vertical line denotes the sample mean for the last 100,000 observations included in the histogram; the green vertical line denotes the value of $ \frac{ {\mathcal B}^*}{E u_c} $, associated with a sample from our approximation to the ergodic distribution where $ {\mathcal B}^* $ is a regression coefficient to be described below; the red vertical line denotes an approximation by [BEGS17] to the mean of the ergodic distribution that can be computed before the ergodic distribution has been approximated, as described below.
Before moving on to discuss the histogram and the vertical lines approximating the ergodic mean of government debt in more detail, the following graphs show government debt and taxes early in the simulation, for periods 1-100 and 101 to 200 respectively.
titles = ['Government Debt', 'Tax Rate']
fig, axes = plt.subplots(4, 1, figsize=(10, 15))
for i, id in enumerate([2, 3]):
axes[i].plot(sim_seq_long[id][:99], '-k', sim_bel_long[id][:99],
'-.b', alpha=0.5)
axes[i+2].plot(range(100, 199), sim_seq_long[id][100:199], '-k',
range(100, 199), sim_bel_long[id][100:199], '-.b',
alpha=0.5)
axes[i].set(title=titles[i])
axes[i+2].set(title=titles[i])
axes[i].grid()
axes[i+2].grid()
axes[0].legend(('Complete Markets', 'Incomplete Markets'))
plt.tight_layout()
plt.show()
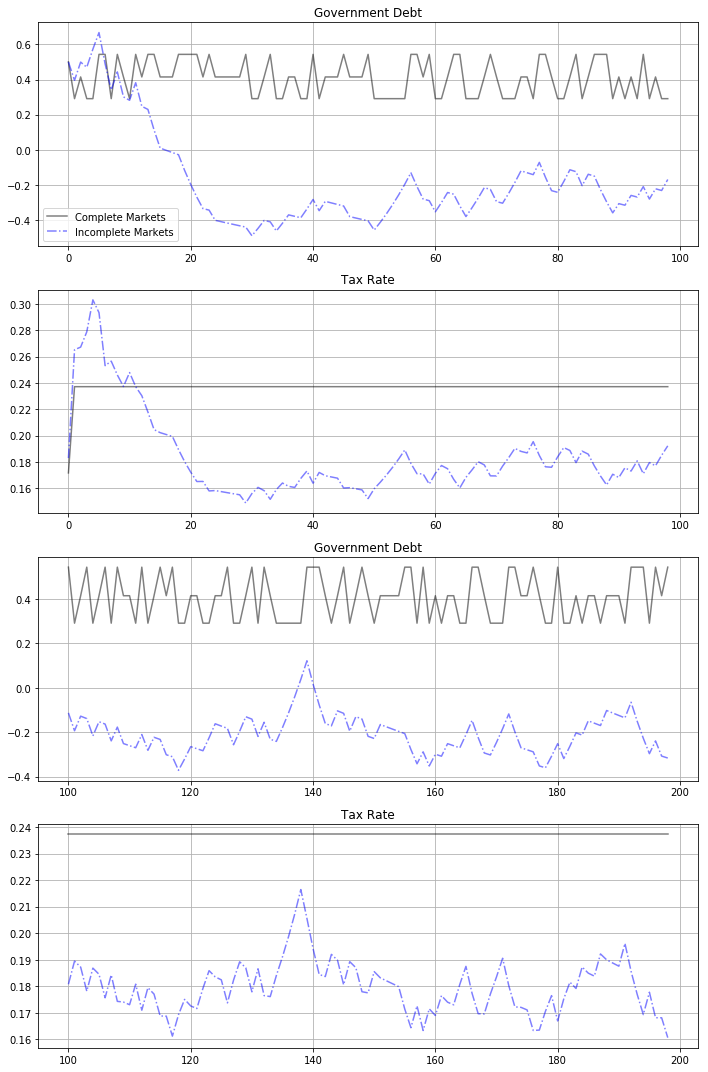
For the short samples early in our simulated sample of 102,000 observations, fluctuations in government debt and the tax rate conceal the weak but inexorable force that the Ramsey planner puts into both series driving them toward ergodic marginal distributions that are far from these early observations
- early observations are more influenced by the initial value of the par value of government debt than by the ergodic mean of the par value of government debt
- much later observations are more influenced by the ergodic mean and are independent of the par value of initial government debt
Asymptotic Mean and Rate of Convergence¶
We apply the results of BEGS [BEGS17] to interpret
- the mean of the ergodic distribution of government debt
- the rate of convergence to the ergodic distribution from an arbitrary initial government debt
We begin by computing objects required by the theory of section III.i of BEGS [BEGS17].
As in Fiscal Insurance via Fluctuating Interest Rates, we recall that BEGS [BEGS17] used a particular notation to represent what we can regard as their generalization of an AMSS model.
We introduce some of the [BEGS17] notation so that readers can quickly relate notation that appears in key BEGS formulas to the notation that we have used in previous lectures here and here.
BEGS work with objects $ B_t, {\mathcal B}_t, {\mathcal R}_t, {\mathcal X}_t $ that are related to notation that we used in earlier lectures by
$$ \begin{aligned} {\mathcal R}_t & = \frac{u_{c,t}}{u_{c,t-1}} R_{t-1} = \frac{u_{c,t}}{ \beta E_{t-1} u_{c,t}} \\ B_t & = \frac{b_{t+1}(s^t)}{R_t(s^t)} \\ b_t(s^{t-1}) & = {\mathcal R}_{t-1} B_{t-1} \\ {\mathcal B}_t & = u_{c,t} B_t = (\beta E_t u_{c,t+1}) b_{t+1}(s^t) \\ {\mathcal X}_t & = u_{c,t} [g_t - \tau_t n_t] \end{aligned} $$BEGS [BEGS17] call $ {\mathcal X}_t $ the effective government deficit and $ {\mathcal B}_t $ the effective government debt.
Equation (44) of [BEGS17] expresses the time $ t $ state $ s $ government budget constraint as
$$ {\mathcal B}(s) = {\mathcal R}_\tau(s, s_{-}) {\mathcal B}_{-} + {\mathcal X}_{\tau} (s) \tag{1} $$
where the dependence on $ \tau $ is meant to remind us that these objects depend on the tax rate; $ s_{-} $ is last period’s Markov state.
BEGS interpret random variations in the right side of (1) as fiscal risks generated by
- interest-rate-driven fluctuations in time $ t $ effective payments due on the government portfolio, namely, $ {\mathcal R}_\tau(s, s_{-}) {\mathcal B}_{-} $, and
- fluctuations in the effective government deficit $ {\mathcal X}_t $
Asymptotic Mean¶
BEGS give conditions under which the ergodic mean of $ {\mathcal B}_t $ is approximated by
$$ {\mathcal B}^* = - \frac{\rm cov^{\infty}({\mathcal R}_t, {\mathcal X_t})}{\rm var^{\infty}({\mathcal R}_t)} \tag{2} $$
where the superscript $ \infty $ denotes a moment taken with respect to an ergodic distribution.
Formula (2) represents $ {\mathcal B}^* $ as a regression coefficient of $ {\mathcal X}_t $ on $ {\mathcal R}_t $ in the ergodic distribution.
Regression coefficient $ {\mathcal B}^* $ solves a variance-minimization problem:
$$ {\mathcal B}^* = {\rm argmin}_{\mathcal B} {\rm var}^\infty ({\mathcal R} {\mathcal B} + {\mathcal X}) \tag{3} $$
The minimand in criterion (3) measures fiscal risk associated with a given tax-debt policy that appears on the right side of equation (1).
Expressing formula (2) in terms of our notation tells us that the ergodic mean of the par value $ b $ of government debt in the AMSS model should be approximately
$$ \hat b = \frac{\mathcal B^*}{\beta E( E_t u_{c,t+1})} = \frac{\mathcal B^*}{\beta E( u_{c,t+1} )} \tag{4} $$
where mathematical expectations are taken with respect to the ergodic distribution.
Rate of Convergence¶
BEGS also derive the following approximation to the rate of convergence to $ {\mathcal B}^{*} $ from an arbitrary initial condition.
$$ \frac{ E_t ( {\mathcal B}_{t+1} - {\mathcal B}^{*} )} { ( {\mathcal B}_{t} - {\mathcal B}^{*} )} \approx \frac{1}{1 + \beta^2 {\rm var}^\infty ({\mathcal R} )} \tag{5} $$
(See the equation above equation (47) in BEGS [BEGS17])
Chicken and Egg¶
Notice how attributes of the ergodic distribution for $ {\mathcal B}_t $ appear on the right side of formula (3) for approximating the ergodic mean via $ {\mathcal B}^* $.
Therefor, formula (3) is not useful for estimating the mean of the ergodic in advance of actually approximating the ergodic distribution.
- we need to know the ergodic distribution to compute the right side of formula (3)
So the primary use of equation (3) is how it confirms that the ergodic distribution solves a fiscal-risk minimization problem.
As an example, notice how we used the formula for the mean of $ {\mathcal B} $ in the ergodic distribution of the special AMSS economy in Fiscal Insurance via Fluctuating Interest Rates
- first we computed the ergodic distribution using a reverse-engineering construction
- then we verified that $ {\mathcal B}^* $ agrees with the mean of that distribution
Approximating the Ergodic Mean¶
BEGS also [BEGS17] propose an approximation to $ {\mathcal B}^* $ that can be computed without first approximating the ergodic distribution.
To construct the BEGS approximation to $ {\mathcal B}^* $, we just follow steps set forth on pages 648 - 650 of section III.D of [BEGS17]
- notation in BEGS might be confusing at first sight, so it is important to stare and digest before computing
- there are also some sign errors in the [BEGS17] text that we’ll want to correct here
Here is a step-by-step description of the BEGS [BEGS17] approximation procedure.
Step by Step¶
Step 1: For a given $ \tau $ we compute a vector of values $ c_\tau(s), s= 1, 2, \ldots, S $ that satisfy
$$ (1-\tau) c_\tau(s)^{-\sigma} - (c_{\tau}(s) + g(s))^{\gamma} = 0 $$This is a nonlinear equation to be solved for $ c_{\tau}(s), s = 1, \ldots, S $.
$ S=3 $ in our case, but we’ll write code for a general integer $ S $.
Typo alert: Please note that there is a sign error in equation (42) of BEGS [BEGS17] – it should be a minus rather than a plus in the middle.
- We have made the appropriate correction in the above equation.
Step 2: Knowing $ c_\tau(s), s=1, \ldots, S $ for a given $ \tau $, we want to compute the random variables
$$ {\mathcal R}_\tau(s) = \frac{c_\tau(s)^{-\sigma}}{\beta \sum_{s'=1}^S c_\tau(s')^{-\sigma} \pi(s')} $$and
$$ {\mathcal X}_\tau(s) = (c_\tau(s) + g(s))^{1+ \gamma} - c_\tau(s)^{1-\sigma} $$each for $ s= 1, \ldots, S $.
BEGS call $ {\mathcal R}_\tau(s) $ the effective return on risk-free debt and they call $ {\mathcal X}_\tau(s) $ the effective government deficit.
Step 3: With the preceding objects in hand, for a given $ {\mathcal B} $, we seek a $ \tau $ that satisfies
$$ {\mathcal B} = - \frac{\beta} {1-\beta} E {\mathcal X_\tau} \equiv - \frac{\beta} {1-\beta} \sum_{s} {\mathcal X}_\tau(s) \pi(s) $$This equation says that at a constant discount factor $ \beta $, equivalent government debt $ {\mathcal B} $ equals the present value of the mean effective government surplus.
Another typo alert: there is a sign error in equation (46) of BEGS [BEGS17] –the left side should be multiplied by $ -1 $.
- We have made this correction in the above equation.
For a given $ {\mathcal B} $, let a $ \tau $ that solves the above equation be called $ \tau(\mathcal B) $.
We’ll use a Python root solver to find a $ \tau $ that solves this equation for a given $ {\mathcal B} $.
We’ll use this function to induce a function $ \tau({\mathcal B}) $.
Step 4: With a Python program that computes $ \tau(\mathcal B) $ in hand, next we write a Python function to compute the random variable.
$$ J({\mathcal B})(s) = \mathcal R_{\tau({\mathcal B})}(s) {\mathcal B} + {\mathcal X}_{\tau({\mathcal B})}(s) , \quad s = 1, \ldots, S $$Step 5: Now that we have a way to compute the random variable $ J({\mathcal B})(s), s= 1, \ldots, S $, via a composition of Python functions, we can use the population variance function that we defined in the code above to construct a function $ {\rm var}(J({\mathcal B})) $.
We put $ {\rm var}(J({\mathcal B})) $ into a Python function minimizer and compute
$$ {\mathcal B}^* = {\rm argmin}_{\mathcal B} {\rm var } (J({\mathcal B}) ) $$Step 6: Next we take the minimizer $ {\mathcal B}^* $ and the Python functions for computing means and variances and compute
$$ {\rm rate} = \frac{1}{1 + \beta^2 {\rm var}( {\mathcal R}_{\tau({\mathcal B}^*)} )} $$Ultimate outputs of this string of calculations are two scalars
$$ ({\mathcal B}^*, {\rm rate} ) $$Step 7: Compute the divisor
$$ div = {\beta E u_{c,t+1}} $$and then compute the mean of the par value of government debt in the AMSS model
$$ \hat b = \frac{ {\mathcal B}^*}{div} $$In the two-Markov-state AMSS economy in Fiscal Insurance via Fluctuating Interest Rates, $ E_t u_{c,t+1} = E u_{c,t+1} $ in the ergodic distribution.
We have confirmed that this formula very accurately describes a constant par value of government debt that
- supports full fiscal insurance via fluctuating interest parameters, and
- is the limit of government debt as $ t \rightarrow +\infty $
In the three-Markov-state economy of this lecture, the par value of government debt fluctuates in a history-dependent way even asymptotically.
In this economy, $ \hat b $ given by the above formula approximates the mean of the ergodic distribution of the par value of government debt
- $ \hat b $ is represented by the red vertical line plotted in the histogram of the last 100,000 observations of our simulation of the par value of government debt plotted above
- the approximation is fairly accurate but not perfect
- so while the approximation circumvents the chicken and egg problem that surrounds
- the much better approximation associated with the green vertical line, it does so by enlarging the approximation error
Execution¶
Now let’s move on to compute things step by step.
Step 1¶
u = CRRAutility(π=(1 / 3) * np.ones((3, 3)),
G=np.array([0.1, 0.2, .3]),
Θ=np.ones(3))
τ = 0.05 # Initial guess of τ (to displays calcs along the way)
S = len(u.G) # Number of states
def solve_c(c, τ, u):
return (1 - τ) * c**(-u.σ) - (c + u.G)**u.γ
# .x returns the result from root
c = root(solve_c, np.ones(S), args=(τ, u)).x
c
root(solve_c, np.ones(S), args=(τ, u))
Step 2¶
n = c + u.G # Compute labor supply
Note about Code¶
Remember that in our code $ \pi $ is a $ 3 \times 3 $ transition matrix.
But because we are studying an IID case, $ \pi $ has identical rows and we need only to compute objects for one row of $ \pi $.
This explains why at some places below we set $ s=0 $ just to pick off the first row of $ \pi $.
Running the code¶
Let’s take the code out for a spin.
First, let’s compute $ {\mathcal R} $ and $ {\mathcal X} $ according to our formulas
def compute_R_X(τ, u, s):
c = root(solve_c, np.ones(S), args=(τ, u)).x # Solve for vector of c's
div = u.β * (u.Uc(c[0], n[0]) * u.π[s, 0] \
+ u.Uc(c[1], n[1]) * u.π[s, 1] \
+ u.Uc(c[2], n[2]) * u.π[s, 2])
R = c**(-u.σ) / (div)
X = (c + u.G)**(1 + u.γ) - c**(1 - u.σ)
return R, X
c**(-u.σ) @ u.π
u.π
We only want unconditional expectations because we are in an IID case.
So we’ll set $ s=0 $ and just pick off expectations associated with the first row of $ \pi $
s = 0
R, X = compute_R_X(τ, u, s)
Let’s look at the random variables $ {\mathcal R}, {\mathcal X} $
R
mean(R, s)
X
mean(X, s)
X @ u.π
Step 3¶
def solve_τ(τ, B, u, s):
R, X = compute_R_X(τ, u, s)
return ((u.β - 1) / u.β) * B - X @ u.π[s]
Note that $ B $ is a scalar.
Let’s try out our method computing $ \tau $
s = 0
B = 1.0
τ = root(solve_τ, .1, args=(B, u, s)).x[0] # Very sensitive to initial value
τ
In the above cell, B is fixed at 1 and $ \tau $ is to be computed as a function of B.
Note that 0.2 is the initial value for $ \tau $ in the root-finding algorithm.
Step 4¶
def min_J(B, u, s):
# Very sensitive to initial value of τ
τ = root(solve_τ, .5, args=(B, u, s)).x[0]
R, X = compute_R_X(τ, u, s)
return variance(R * B + X, s)
min_J(B, u, s)
Step 6¶
B_star = minimize(min_J, .5, args=(u, s)).x[0]
B_star
n = c + u.G # Compute labor supply
div = u.β * (u.Uc(c[0], n[0]) * u.π[s, 0] \
+ u.Uc(c[1], n[1]) * u.π[s, 1] \
+ u.Uc(c[2], n[2]) * u.π[s, 2])
B_hat = B_star/div
B_hat
τ_star = root(solve_τ, 0.05, args=(B_star, u, s)).x[0]
τ_star
R_star, X_star = compute_R_X(τ_star, u, s)
R_star, X_star
rate = 1 / (1 + u.β**2 * variance(R_star, s))
rate
root(solve_c, np.ones(S), args=(τ_star, u)).x
